Tuesday, February 14, 2012
Alyssa's Pythagorean Relationship Post
Pythagorean Relationship: a2 + b2 = c2
a2 - is one of the legsc2 - is the hypotenuse of a right triangle
2. Answer the missing side.
one leg equals = 12 which is A side
the other = 5
so we go c=a+b
c2=12+5
c2= (12x12) + (5x5)
c2= 144+25
c2=169( sqaure root it )
c=13
so the answer will be the c= 13 2
3.is the triangle a right triangle? prove it !!!
a or b = 8
the other side (a or b) = 6
a2+b2=c2
8+6=14
14(2)=11(2)
the triangle is not a right triangle
b2 - is also one of the legs
Steven's pythagorean relationship texbook questions (4,10,15)

1) Answer in a short paragraph with diagrams



pythagorean relationship

a² and b² are equal to form the hypotenuse.
2. Solve for the missing side length.

13cm
3. Is this a right triangle? Prove it!!!

Jay's Pythagorean Relationship


13cm

Monday, February 13, 2012
Liyanah's Pythagorean Post

a² + b² = c²:
The Pythagorean Relationship means that the two legs (a & b) both equal to the hypotenuse. So for example we had the two legs (a &b) which are 3 and 4, and the hypotenuse is 5. Now you use the Pythagorean Relationship which is a² + b² = c² and put the numbers in now so this is how the steps would go:
a² + b² = c²
3² + 4² = 5²
(3x3) + (4x4) = (5x5)
9cm + 16cm = 25cm
25 = 25 - therefore, it is a right triangle
Here is a picture of what the triangle looks like:


My answer:

3. Is this a right triangle? Prove it!!!

My answer:

Charisse's Pythagorean Relationship

a(squared) + b(squared) = C(squared)
This Pythagorean Relationship means that the legs of the right triangle together equals to the hypotenuse, which is the longest side length of the right triangle. Say if the side lengths of the right triangle (A and B) were 4 and 3 and the hypotenuse (C) was 5. You would sub the letters to numbers.. so it would be 4(squared) + 3(squared) = 5(squared). Squared means to times it's number by it self, so it would be 4x4+3x3=5x5. So now you multiply the numbers, 4x4=16, 3x3=9, 5x5=25. 16+9=25, Both of the legs together equals to the hypotenuse, therefore it is a right triangle.
2. Solve for the missing side length.


3. Is this a right triangle? Prove it!!!


Pythagorean Relationship
a2+b2=c2
a2+b2 = c2 because the 2 legs are smaller than the hypotenuse and for it to equal c2, you have to square a2 and b2 and square root it after to get the hypotenuse(c2).
2.c2=a2+b2
c2=122+5cm2
c2=(12x12)+(5x5)
c2=144+25
c2=169cm2
square root 169= 13cm
3.Is this a right triangle?
a2+b2=c2
82+62=112
(8x8)+(6x6)=(11x11)
64+36 does not equal 121
So It is not a right triangle.
Pythagorean Scribe/ Textbook pythagorean questions
1. Explain what the pythagorean relationship.
a2+b2=c2
a2+b2 = c2 because the 2 legs are smaller than the hypotenuse and for it to equal c2, you have to square a2 and b2 and square root it after to get the hypotenuse(c2).
a= 5cm b= 12cm c=?
c2=a2+b2
c2=5cm2+ 12cm2
c2=(5x5)+(12x12)
c2=25+144
c2= 169cm2
c=13cm
3. Is this a right triangle? Prove it!
a=6cm b=8cm c=11cm
a2+b2=c2
6cm2+8cm2= 11cm2
(6x6)+(8x8)=(11x11)
36+64=100
c=10
It is not a right triangle because it doesn't equal the hypotenuse.
Textbook Questions pg. 92-93 # 5,9,13
5.A right triangle has side lengths of 40mm, 75mm, and 85mm.
a)Sketch the triangle. Draw a square on each side of the triangle.

b)What are the areas of the three squares.
b)40mm= 40x40= 1,600
75x75= 5,625
85x85= 7,225
c)Write an addition statement with the areas of the three squares.
c) 1600+5625+7226= 14,451 mm
9.Calculate the areas of the three squares
4cm= 4x4=16cm
2x2= 4cm
3x3= 9cm

b) Is this triangle a right triangle? Explain.
b) No because 2+3 cm squared has to equal 4cm squared but it does not. 9+4 does not equal 16.
13. A small triangular flower bed has a square stepping stone at each of its sides. Is the flower bed in the shape of a right triangle? Explain your reasoning.

It is not a right triangle because the 2 legs (4800cm) has to equal the hypotenuse (9800cm) if u add them up. 4800+4800=9600 cm
not 9800cm.
Kamille's Pythagorean Post
YES!
Elijah's Pythagorean Post
Oudorn's Textbook Questions (12,14,17)
a)Estimate the side length of the rug, to one decimal place

b)Check your estimate with a calculator.
Square root of 11=3.316
c) Will the rug fit? Explain.
Yes it will, because the area of the room is 20m²
14. Alex is thinking of a number. The number has a square root between 7 and 8, and a multiple of 12.
a) What number could he be thinking of?
60
b) Is there more than one answer? Explain.
No, because 60 is the only number that is between the square root of 7 and 8 that is a multiple of 12.
17. Carmel wants to mount an 18cm x 18cm square picture on a square board that is four times the area or the picture
a) What is the area of the picture?

b) What is the area of the board?
324 x 324 = 1296cm²
Square root of 1296= 36cm
a² + b² = c² is a formula. If you take the legs of the triangle( a and b), square them, then add them, you will get c²(hypotenuse²). You can determain if the triangle is a right triangle or not by doing a² + b² = c².
C²=(5x5)+(12x12)
C²=25+144
C²=169
C= square root of 169
C= 13cm

Pythagoras + Textbook Questions


Adrian's Pythagorean Relationship Post
1. Answer in a short paragraph and with diagrams
The two legs Leg A and Leg B are equal to c which is called the hypotenuse.
2.Solve the missing side length
a+b=c
a=(12x12)+(5x5)
a=(144)(25)
a=144+25=169cm
missing side length=169cm2
a+b=c
It is not a right triangle because the legs arent equal to the hypotenuse.
Textbook Questions
19. estimate the square root of 160 100
square root of 100 =40
square root of 160=10
10x40=400
6. What is an example of a whole number that has a square root
between 9 and 10. answer 81
Diana's Pythagorean Relationship


For this first question, I'm going to be writing about Pythagorean Relationship and show a diagram. A Pythagorean relationship can be used to determine whether a triangle is a right triangle or not. The "a²" and "b²" are called the "legs". The "c" stands for " hypotenuse". To find the side length "a" you use a²= c² - b²; for b, you use b²= c² - a² and for "c" you use c²= a² + b². These are some facts that I know about Pythagorean Relationship.
2. Solve for the missing side length.


3. Is this a right triangle? Prove it!!!


Nikko phythagorean
3.3. Is this a right triangle? Prove it!!!
Terence's Pythagoras Scribe Edit

1. Answer a short paragraph with diagrams.

Pythagorean relationship part 2
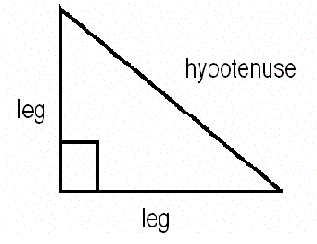
Patricia's Pythagorean Post
The relationship between the lengths of the side of the right triangle. The sum of the areas of the squares attached to the legs of a right triangle equals the area of a square attached to the hypotenuse.

the Pythagorean relationship can be used to show if a triangle is a right triangle. Left side: 7 squared+6 square= 13 squared (7x7)+(6x6)=(13x13) 49+36=85 square root of "C" squared= square root of 100cm squared is 10
C=10cmthe sum of the areas of the two smaller squares is 100cm squared. the triangle is a right triangle.
2.Solve the missing side length

a squared+b squared= c squared 8 squared+6 squared=11 squared (8x8)+(6x6)=(11x11) 64+36=121 square root of "C"squared= square root of 121cm squared is 11
C=11cm
the triangle a right triangle.
3. Is this a right triangle? Prove it!!!

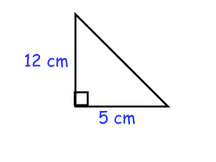
a squared + b squared = c squared
8 squared + 6 squared = 11 squared
(8x8) + (6x6) = (11x11)
64 + 36 = 121
It's not a right triangle because it's not equal. The legs aren't equal to the hypotenuse.
Textbook Questions
5.a) What is the area of each square attached?
a squared = 6 squared
a squared = 6 x 6
b squared = 8
squared
b squared = 8 x
8
b squared
= 64 cm squared
b) c squared = a squared + b
squared
c squared = 36 + 64
c squared = 100 cm squared
c) square root "c" squared and then square root 100 cm
squared
c = 10 cm
19. estimate the square root of 160 100
square root of 100 =40
square root of 160=10
10x40=400
14.
Alex is thinking of a number. The number has a square root between 7 and 8, and
a multiple of 12.
a) What number could he be thinking of?60
b) Is there more than one answer?
Explain.
No, because 60 is the only number that is between the square root of
7 and 8 that is a multiple of 12.