Alyssa's Pythagorean Relationship Post

1. Explain the pythagorean relationship.

Pythagorean Relationship: a2 + b2 = c2

a2 - is one of the legsc2 - is the hypotenuse of a right triangle

2. Answer the missing side.
one leg equals = 12 which is A side
the other = 5
so we go c=a+b
c2=12+5
c2= (12x12) + (5x5)
c2= 144+25
c2=169( sqaure root it )
c=13
so the answer will be the c= 13 2

3.is the triangle a right triangle? prove it !!!
a or b = 8 
the other side (a or b) = 6
a2+b2=c2
8+6=14
14(2)=11(2)
the triangle is not a right triangle
b2 - is also one of the legs

Steven's pythagorean relationship texbook questions (4,10,15)

4) Estimate the square root of each number, to one decimal. Check with a calculator.

a) 72 b) 103 c) 55

10. Kai uses an entire can of paint on a square backdrop for the school play. The label on the can states that one can cover 27 m² of wall surface. Estimate the backdrop's side length, to one decimal place.

.

5x5=25 and 6x6=36 so it should be between the numbers 5 and 6.

5.2x5.2=27.04 then it move it up into one decimal place which is 5.3

15. Order the following numbers from least to greatest: 7, square root of 46, 5.8, square root of 27, and 6.3.

5.1, 5.8, 6.3, 6.7, 7






1) Answer in a short paragraph with diagrams

pythagorean relationship

1. Answer in a short paragraph and with diagrams

a² and b² are equal to form the hypotenuse.

2. Solve for the missing side length.


13cm

3. Is this a right triangle? Prove it!!!

No because the sum of area of the smaller sides (legs) are not equal to the largest

Jay's Pythagorean Relationship

1. Answer in a short paragraph and with diagrams

Both a2 and b2 are equal to find the side length of the hypotenuse.

2. Solve for the missing side length.


13cm

3. Is this a right triangle? Prove it!!!

No. Both legs are not equal to hypotenuse.

Liyanah's Pythagorean Post

1. Answer in a short paragraph and with diagrams





a² + b² = c²:
The Pythagorean Relationship means that the two legs (a & b) both equal to the hypotenuse. So for example we had the two legs (a &b) which are 3 and 4, and the hypotenuse is 5. Now you use the Pythagorean Relationship which is a² + b² = c² and put the numbers in now so this is how the steps would go:

a² + b² = c²
3² + 4² = 5²
(3x3) + (4x4) = (5x5)
9cm + 16cm = 25cm
25 = 25 - therefore, it is a right triangle

Here is a picture of what the triangle looks like:

2. Solve for the missing side length.










My answer:








3. Is this a right triangle? Prove it!!!










My answer:

Charisse's Pythagorean Relationship

1. Answer in a short paragraph and with diagrams



a(squared) + b(squared) = C(squared)
This Pythagorean Relationship means that the legs of the right triangle together equals to the hypotenuse, which is the longest side length of the right triangle. Say if the side lengths of the right triangle (A and B) were 4 and 3 and the hypotenuse (C) was 5. You would sub the letters to numbers.. so it would be 4(squared) + 3(squared) = 5(squared). Squared means to times it's number by it self, so it would be 4x4+3x3=5x5. So now you multiply the numbers, 4x4=16, 3x3=9, 5x5=25. 16+9=25, Both of the legs together equals to the hypotenuse, therefore it is a right triangle.

2. Solve for the missing side length.

3. Is this a right triangle? Prove it!!!

Pythagorean Relationship

1. Explain what the pythagorean relationship.
a2+b2=c2
a2+b2 = c2 because the 2 legs are smaller than the hypotenuse and for it to equal c2, you have to square a2 and b2 and square root it after to get the hypotenuse(c2).

2.c2=a2+b2
c2=122+5cm2
c2=(12x12)+(5x5)
c2=144+25
c2=169cm2
square root 169= 13cm

3.Is this a right triangle?

a2+b2=c2
82+62=112
(8x8)+(6x6)=(11x11)
64+36 does not equal 121
So It is not a right triangle.

Pythagorean Scribe/ Textbook pythagorean questions

1. Answer in a short paragraph and with diagrams

1. Explain what the pythagorean relationship.
a2+b2=c2
a2+b2 = c2 because the 2 legs are smaller than the hypotenuse and for it to equal c2, you have to square a2 and b2 and square root it after to get the hypotenuse(c2).

2. Solve for the missing side length.

a= 5cm b= 12cm c=?
c2=a2+b2
c2=5cm2+ 12cm2
c2=(5x5)+(12x12)
c2=25+144
c2= 169cm2
c=13cm

3. Is this a right triangle? Prove it!

a=6cm b=8cm c=11cm
a2+b2=c2
6cm2+8cm2= 11cm2
(6x6)+(8x8)=(11x11)

36+64=121
36+64=100
c=10

It is not a right triangle because it doesn't equal the hypotenuse.


Textbook Questions pg. 92-93 # 5,9,13

5.A right triangle has side lengths of 40mm, 75mm, and 85mm.

a)Sketch the triangle. Draw a square on each side of the triangle.
b)What are the areas of the three squares.

b)40mm= 40x40= 1,600
75x75= 5,625
85x85= 7,225

c)Write an addition statement with the areas of the three squares.

c) 1600+5625+7226= 14,451 mm

9.Calculate the areas of the three squares

4cm= 4x4=16cm
2x2= 4cm
3x3= 9cm

b) Is this triangle a right triangle? Explain.
b) No because 2+3 cm squared has to equal 4cm squared but it does not. 9+4 does not equal 16.

13. A small triangular flower bed has a square stepping stone at each of its sides. Is the flower bed in the shape of a right triangle? Explain your reasoning.

It is not a right triangle because the 2 legs (4800cm) has to equal the hypotenuse (9800cm) if u add them up. 4800+4800=9600 cm
not 9800cm.

Kamille's Pythagorean Post

1. Answer in a short paragraph and with diagrams

You can use the Pythagorean relationship to know if a triangle is right triangle or not. The "a" and "b" on a right triangle represents the legs. The "c" is called the hypotenuse. If you add both side lengths of a and b you will get the hypotenuse. You can also determine a missing side length using one of this formulas

a²= c² - b²

b²= c² - a²

c²= a² +b²

2. Solve for the missing side length.

c²= a² +b²

c²= 12cm+5cm

c²= (12x12)+(5x5)

c²= 144cm²+25cm²

c²= 169cm²

√ c² = 169cm²

√ c  = 13cm

3. Is this a right triangle? Prove it!!!

YES!

c²= a² +b²

c²= 8cm+6cm

c²= (8x8)+(6x6)

c²= 64cm²+36cm²

c²= 100cm²

√ c² = 100cm²

√ c  = 10cm

Elijah's Pythagorean Post

1. Answer in a short paragraph and with diagrams

The Pythagorean Relationship is a right triangle that consists of a hypotenuse and two legs. The hypotenuse is ALWAYS larger than the two legs but when the two legs are summed up it equals the hypotenuse.

2. Solve for the missing side length

a squared + b squared= c squared

12cm squared + 5cm squared= c squared

(12x12) + (5x5)= c squared

144 + 25= 169cm squared

c squared= 169 squared

c=14cm

3. Is this a right triangle? Prove it!!

a squared + b squared= c squared

8cm squared + 6cm squared= 11cm squared

(8x8) + (6x6)= 11cm squared

64cm squared + 36cm squared= 11cm squared

c squared= 100 squared cm

c= 10cm

No it is not a right triangle

Oudorn's Textbook Questions (12,14,17)

12. While shopping online, Ji Hun finds a square rug with the area of 11 m squared. He needs to know if it will fit his 4m x 5m bedroom.

a)Estimate the side length of the rug, to one decimal place














b)Check your estimate with a calculator.

Square root of 11=3.316

c) Will the rug fit? Explain.
Yes it will, because the area of the room is 20m²

14. Alex is thinking of a number. The number has a square root between 7 and 8, and a multiple of 12.

a) What number could he be thinking of?

60

b) Is there more than one answer? Explain.
No, because 60 is the only number that is between the square root of 7 and 8 that is a multiple of 12.

17. Carmel wants to mount an 18cm x 18cm square picture on a square board that is four times the area or the picture

a) What is the area of the picture?

Area = 324cm²

b) What is the area of the board?

324 x 324 = 1296cm²

c) What are the dimensions of the board?

Square root of 1296= 36cm

36 x 36 = 1296cm²

Pythagorean Relationship

1.Answer in short paragraph and with diagrams

a² + b² = c² is a formula. If you take the legs of the triangle( a and b), square them, then add them, you will get c²(hypotenuse²). You can determain if the triangle is a right triangle or not by doing a² + b² = c².

2. Solve for the missing side length.

C²= A²(5cm)+B²(12cm)

C²=5²+12²
C²=(5x5)+(12x12)
C²=25+144
C²=169
C= square root of 169
C= 13cm

3.Is this a right triangle? Prove it!!!

Pythagoras + Textbook Questions

Adrian's Pythagorean Relationship Post

1. Answer in a short paragraph and with diagrams
The two legs Leg A and Leg B are equal to c which is called the hypotenuse.

2.Solve the missing side length
a+b=c
a=(12x12)+(5x5)
a=(144)(25)
a=144+25=169cm
missing side length=169cm2

3.Is it a right triangle?

a+b=c

(8x8)+(6x6=(11x11)

64+36=121

It is not a right triangle because the legs arent equal to the hypotenuse.

Textbook Questions

19. estimate the square root of 160 100

square root of 100 =40
square root of 160=10

10x40=400

6. What is an example of a whole number that has a square root
between 9 and 10. answer 81

Diana's Pythagorean Relationship

1. Answer in a short paragraph and with diagrams


For this first question, I'm going to be writing about Pythagorean Relationship and show a diagram. A Pythagorean relationship can be used to determine whether a triangle is a right triangle or not. The "a²" and "b²" are called the "legs". The "c" stands for " hypotenuse". To find the side length "a" you use a²= c² - b²; for b, you use b²= c² - a² and for "c" you use c²= a² + b². These are some facts that I know about Pythagorean Relationship.

2. Solve for the missing side length.

3. Is this a right triangle? Prove it!!!

Nikko phythagorean

1. Answer in a short paragraph and with diagrams

The a and b represents the legs and the c is the hypotenuse.When you add

a and b you will get the hypotenuse.




2. a2+b2=c2
c2=a2+b2
c2=122+52
c2=(12x12)+(5x5)
c2=144+25
c2=169

c2=13

3.3. Is this a right triangle? Prove it!!!

c=a2+b2

c=82+62

c=(8x8)X(6x6)

c=64+36=11 cm

c=100

c=10

NO it is not a right triangle!!

Terence's Pythagoras Scribe Edit

1. Answer a short paragraph with diagrams.

Explain the Pythagorean Relationship.

The two legs which are A and B equal the hypotenuse which is C. The C may also equal A or B if you subtract. If you subtract C with A it may equal the B and

the same thing goes for C-B. If you do A+B=C, B=A-C, and A=B-C it will show if you have a right triangle and those are the formulas.

2. Solve the missing side length

A=12 cm

B=5 cm

A+B=C

(12x12)+(5x5)=

144+25=169

C=169cm2

C=13

3. Is this a right triangle? Prove it!!!

A=8 cm

B=6 cm

C=11 cm

A+B=C

(8x8)+(6x6)=(11x11)

64+36=(100) 121

It is not a right triangle because 64+36=100 not 121.

Pythagorean relationship part 2

I am going to show you what C2= A2+B2 is:

C2 is the hyptenuse of a right triangle also known as the longer part of it.

A2 is one of the legs in a right triangle which is the height of it.

B2 is the other leg of the right trangle known as the base which tells how long it is.

How you find the hypotenuse is take the A2 + B2 and it gives you a higher number, but you have to square root the number to get a answer.

example is:C2=A2+B2

C2=15cm2 + 39cm2

C2=225cm + 1521cm

C2= 1746

(C2= (1746

C2= 41cm

Patricia's Pythagorean Post

1. Answer in a short paragraph and with diagrams
The relationship between the lengths of the side of the right triangle. The sum of the areas of the squares attached to the legs of a right triangle equals the area of a square attached to the hypotenuse.




the Pythagorean relationship can be used to show if a triangle is a right triangle. Left side: 7 squared+6 square= 13 squared (7x7)+(6x6)=(13x13) 49+36=85 square root of "C" squared= square root of 100cm squared is 10
C=10cmthe sum of the areas of the two smaller squares is 100cm squared. the triangle is a right triangle.

2.Solve the missing side length

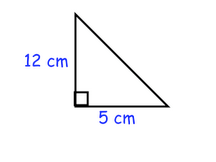
a squared+b squared= c squared 8 squared+6 squared=11 squared (8x8)+(6x6)=(11x11) 64+36=121 square root of "C"squared= square root of 121cm squared is 11
C=11cm
the triangle a right triangle.

3. Is this a right triangle? Prove it!!!

a squared + b squared = c squared
8 squared + 6 squared = 11 squared
(8x8) + (6x6) = (11x11)
64 + 36 = 121
It's not a right triangle because it's not equal. The legs aren't equal to the hypotenuse.

Textbook Questions

5.a) What is the area of each square attached?

a squared = 6 squared

a squared = 6 x 6

a squared = 36 cm squared

b squared = 8
squared

b squared = 8 x
8

b squared
= 64 cm squared

b) c squared = a squared + b
squared

c squared = 36 + 64

c squared = 100 cm squared

c) square root "c" squared and then square root 100 cm
squared

c = 10 cm

19. estimate the square root of 160 100

square root of 100 =40

square root of 160=10

10x40=400

14.

Alex is thinking of a number. The number has a square root between 7 and 8, and
a multiple of 12.

a) What number could he be thinking of?60

b) Is there more than one answer?
Explain.

No, because 60 is the only number that is between the square root of
7 and 8 that is a multiple of 12.