Patricia's Pythagorean Post

1. Answer in a short paragraph and with diagrams
The relationship between the lengths of the side of the right triangle. The sum of the areas of the squares attached to the legs of a right triangle equals the area of a square attached to the hypotenuse.




the Pythagorean relationship can be used to show if a triangle is a right triangle. Left side: 7 squared+6 square= 13 squared (7x7)+(6x6)=(13x13) 49+36=85 square root of "C" squared= square root of 100cm squared is 10
C=10cmthe sum of the areas of the two smaller squares is 100cm squared. the triangle is a right triangle.

2.Solve the missing side length

a squared+b squared= c squared 8 squared+6 squared=11 squared (8x8)+(6x6)=(11x11) 64+36=121 square root of "C"squared= square root of 121cm squared is 11
C=11cm
the triangle a right triangle.

3. Is this a right triangle? Prove it!!!

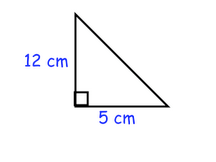
a squared + b squared = c squared
8 squared + 6 squared = 11 squared
(8x8) + (6x6) = (11x11)
64 + 36 = 121
It's not a right triangle because it's not equal. The legs aren't equal to the hypotenuse.

Textbook Questions

5.a) What is the area of each square attached?

a squared = 6 squared

a squared = 6 x 6

a squared = 36 cm squared

b squared = 8
squared

b squared = 8 x
8

b squared
= 64 cm squared

b) c squared = a squared + b
squared

c squared = 36 + 64

c squared = 100 cm squared

c) square root "c" squared and then square root 100 cm
squared

c = 10 cm

19. estimate the square root of 160 100

square root of 100 =40

square root of 160=10

10x40=400

14.

Alex is thinking of a number. The number has a square root between 7 and 8, and
a multiple of 12.

a) What number could he be thinking of?60

b) Is there more than one answer?
Explain.

No, because 60 is the only number that is between the square root of
7 and 8 that is a multiple of 12.